
문제
https://www.acmicpc.net/problem/10830
개념
수학, 분할 정복
실행 결과

구현 코드(c++)
#include <iostream>
#include <vector>
using namespace std;
const long long MOD = 1000; // 모듈러 연산용 상수
struct Matrix {
vector<vector<long long>> m;
int size;
// 행렬크기 n으로 초기화
Matrix(int n) : size(n) { m.resize(n, vector<long long>(n)); }
// 연산자 오버로딩 - 행렬 곱셈
Matrix operator*(const Matrix& mm) {
Matrix result(size);
for (int i = 0; i < size; i++) {
for (int j = 0; j < size; j++) {
result.m[i][j] = 0;
for (int k = 0; k < size; k++) {
result.m[i][j] += (m[i][k] * mm.m[k][j]) % MOD;
result.m[i][j] %= MOD;
}
}
}
return result;
}
};
// 거듭제곱용 함수
Matrix pow(Matrix base, long long exp) {
int size = base.size;
Matrix result(size);
for (int i = 0; i < size; i++) {
result.m[i][i] = 1;
}
while (exp > 0) {
if (exp % 2 == 1) {
result = result * base;
}
base = base * base;
exp /= 2;
}
return result;
}
int main() {
ios_base::sync_with_stdio(false);
cin.tie(nullptr);
cout.tie(nullptr);
int n;
long long b;
cin >> n >> b;
Matrix M(n);
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
cin >> M.m[i][j];
}
}
Matrix result = pow(M, b);
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
cout << result.m[i][j] << " ";
}
cout << "\n";
}
return 0;
}
코드 설명
먼저 단순히 말 그대도 구현해서는 해결할 수 없는 문제임에 유의하자.
왜냐하면 거듭제곱이므로 연산할 수 없을 정도로 커지게 될 수 있다.
따라서 문제에서도 1000으로 나눈 나머지 연산을 사용하라고 일러주고 있다.
이 문제를 해결하기 위해서는 행렬의 곱셈을 어떻게 구현할 것인가에 달려있다.
여러 방법이 있겠지만 연산자 오버로딩을 사용해 구조체에 곱셈(*) 연산을 사용할 수 있도록 선언하고, 이에 따라 코드를 구현했다.
행렬 곱셈
2*2 크기의 행렬 곱셈을 생각해보면 다음과 같이 동작한다.
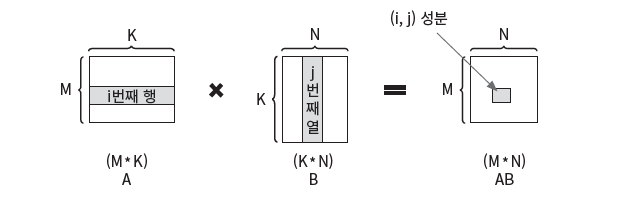
즉, 두 개의 행렬을 곱할 때, 첫 번째 행렬의 각 행과 두 번째 행렬의 각 열을 차례대로 곱해서 더해주는 과정이다.
하지만 이 문제는 행렬 크기인 n을 동적으로 입력받아야 한다.
따라서 행렬 크기에 따른 행, 열 정보를 i,j변수로 성분을 표현하여 구현해야 한다.
단위 행렬이란?
단위행렬은 보통 I로 나타내며, 대각선 숫자만 1이고 나머지 숫자들은 0으로 이뤄진 행렬이다.
곱셈 시 그대로 해당 행렬이 나오게 하는 행렬로, 일반적인 숫자의 1과 같다고 생각하면 된다.
따라서 어떤 행렬 V가 있을때, V * I를 하면 그대로 V가 나오게 된다.
for (int i = 0; i < size; i++) {
result.mat[i][i] = 1; // 대각선에 있는 모든 원소를 1로 정의
}
c++ 코드로는 위와 같이 구현할 수 있다.
연산자 오버로딩을 통한 행렬 구조체 곱셈
for (int i = 0; i < size; i++) { // 첫 번째 행렬의 행을 선택
for (int j = 0; j < size; j++) { // 두 번째 행렬의 열을 선택
result.m[i][j] = 0; // 결과값을 저장할 자리
for (int k = 0; k < size; k++) { // A의 열과 B의 행을 차례대로 곱하는 부분
result.m[i][j] += (m[i][k] * mm.m[k][j]) % MOD; // 곱해서 더함
result.m[i][j] %= MOD; // 1000으로 나눈 나머지를 저장
}
}
}
행을 i, 열을 j 성분이라고 하고 n*n차원 크기의 행렬벡터 m을 미리 선언해둔다.
곱한 결과를 저장할 변수 result에 ik와 kj를 곱한 값을 전부 더해서 1000으로 나눈다.
여기서 k는 0부터 n-1의 값으로, 특정 행과 특정 열을 차례로 곱하기 위한 temp값? 정도로 쓰이는 변수라고 보면 된다.
'PS' 카테고리의 다른 글
| [프로그래머스] 문자열 여러 번 뒤집기 (0) | 2024.10.10 |
|---|---|
| [프로그래머스] 주사위 게임 3 (2) | 2024.10.09 |
| [백준] 2178번: 미로 탐색 (7) | 2024.10.01 |
| [코드트리] 행복한 수열의 개수 (1) | 2024.09.29 |
| [백준] 1260번: DFS와 BFS (0) | 2024.09.29 |