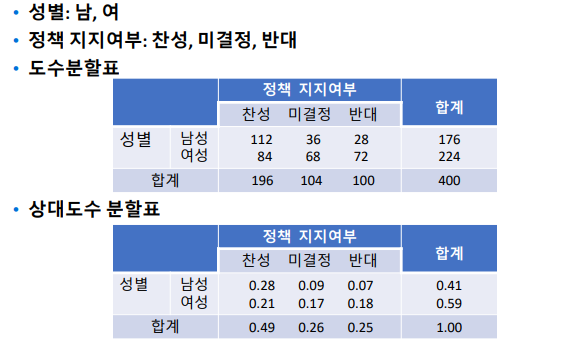
분할표
두 변수가 모두 범주형인 경우 사용
산점도
두 변수가 모두 연속형인 경우 사용

표준상관계수(Pearson correlation)
산점도에서 점들이 얼마나 직선에 가까운지 나타냄 => 선형관계인가 아닌가
r = 두 변수의 편차들의 곱의 합 / 각각 편차들의 합 = 공분산 / 각각 변수의 표준편차
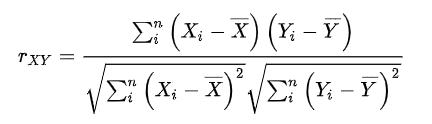
-1 < r < 1
r의 크기는 직선관계에 가까운 정도를 나타냄
r 값만 보고 선형관계가 무조건 크다 작다를 판별할 수 없음
상관계수가 크다고 해서 인과관계가 있다는 건 아니다! (잠재변수 고려해야 함)
심슨의 역설
각각의 변수를 고려하지 않고 전체 통계 결과만을 이용해 결론을 도출할 경우 발생할 수 있는 오류
평균의 함정: 처음 결과와 반대되는 역설적 상황 발생
'Statistics' 카테고리의 다른 글
| 통계학 - 표집분포 (0) | 2022.05.08 |
|---|---|
| 통계학 (0) | 2022.04.16 |
| 통계학 - 수치를 통한 연속형 자료의 요약 (0) | 2022.04.12 |
| 통계학 - 표와 그림을 통한 자료의 요약 기초 (0) | 2022.04.12 |
| 통계학 - 결합분포 (0) | 2022.04.12 |