자료의 요약 방법
- 수치형(양적 자료): 관측되는 값이 수치로 측정됨. 자료의 크기 중요 => 연속, 이산
- 범주형(질적 자료): 관측되는 값이 범주로 나타남. 자료의 내용 중요 => 순위, 명목
범주형 자료
몇 개의 범주가 반복해서 나타남
전체 자료 중 각 범주에 속하는 자료의 횟수(도수)를 요약
- 순위형 자료: 범주 간 순서가 있음 ex. 평점, 선호도
- 명목형 자료: 순서의 의미가 없음 ex. 혈액형, 성별, 고향 등
범주형 자료의 요약 (1) 도수분포표
범주와 그에 대응하는 도수와 상대도수를 나열한 표
도수: 각 범주에 속하는 관측값의 "개수"
상대도수: 도수를 자료의 전체 개수로 나눈 "비율"

범주형 자료의 요약 (2) 원형그래프
원을 상대도수에 비례하도록 중심각을 나누어 파이 조각처럼 나타낸 것
- 장점: 비율 비교 쉬움
- 단점: 도수 비교 어려움
범주형 자료의 요약 (3) 막대그래프
각 범주에서 도수의 크기를 막대의 높이로 나타낸 그림
- 장점: 도수 비교 쉬움
- 단점: 비율 비교 어려움
범주형 자료의 요약 (4) 파레토그림
각 범주에서 도수의 크기를 막대의 높이로 나타낸 그림
상대 도수의 크기가 큰 순서로 범주를 왼쪽부터 오른쪽으로 배열
누적상대도수(왼쪽 범주들까지의 상대도수합)를 각 범주의 막대 위 중앙에 표시하고 그 점들을 연결
- 장점: 중요한 범주 파악 쉬움
- 단점: 순위형 자료에는 유용하지 않음

수치형 자료
- 연속형 자료: 관측 가능한 값이 연속적임 ex. 키, 몸무게 등
- 이산형 자료: 관측 가능한 값이 셀 수 있음 ex. 주사위의 결과, 교통사고 건수 등
이산형 자료의 요약
관측값의 종류가 많은 경우: 연속형 자료를 요약하는 방법을 사용 ex. 도수분포표, 막대그래프 등...
관측값의 종류가 적은 경우: 범주형 자료를 요약하는 방법을 사용 (단, 파레토그림은 적절하지 않음)
연속형 자료의 요약 (1) 점도표
모든 자료를 나타낼 수 있는 수평선을 긋고 눈금을 표시하고 각 관측값에 해당하는 위치에 점을 찍어 표시 • 이미 점이 표시되어 있으면 그 점 위에 다른 점을 표시
- 장점: 자료의 분포 특징을 쉽게 파악할 수 있음
- 단점: 자료의 수가 많은 경우에는 적절하지 않음

연속형 자료의 요약 (2) 도수분포표
- 자료의 범위(최댓값 - 최솟값)를 구하기
- 계급구간의 폭: 계급의 수가 5~15개가 되도록 적절히 조정 (꼭 같은 크기로 작성할 필요 X)
- 계급구간: 관측값이 계급의 경계에 놓이지 않도록 경계점을 구함
- 관측값의 구간에 따라 도수를 셈 => 계급화
- 각 구간에 속하는 관측값의 개수(도수)를 셈
연속형 자료의 요약 (3) 히스토그램
도수분포표를 바탕으로 각 계급에 대한 도수의 크기를 막대로 나타냄
막대의 높이: 상대도수 / 계급구간의 폭
히스토그램의 전체 면적 = 1
- 장점: 자료의 분포를 쉽게 파악
- 단점: 개개의 관측값에 대한 정보를 잃어버림

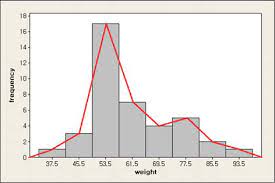
연속형 자료의 요약 (4) 도수다각형
히스토그램에서 각 계급구간의 막대 상단의 중앙점을 직선으로 연결
여러 개 자료를 비교할 때 히스토그램보다 도수다각형이 유용함
- 장점: 자료의 분포를 쉽게 파악
- 단점: 개개의 관측값에 대한 정보를 잃어버림
연속형 자료의 요약 (4) 줄기-잎 그림
관측값을 앞 단위(줄기)와 뒷 단위(잎)로 나누어 나무의 줄기와 잎 모양으로 나타낸 그림
- 장점: 원래 관측값을 보여주므로 최댓값, 최솟값 등을 파악하기 쉬움
- 단점: 자료의 개수가 많거나, 지나치게 흩어져 있는 경우 적절하지 않음
'Statistics' 카테고리의 다른 글
| 통계학 - 두 변수 자료의 요약 (0) | 2022.04.12 |
|---|---|
| 통계학 - 수치를 통한 연속형 자료의 요약 (0) | 2022.04.12 |
| 통계학 - 결합분포 (0) | 2022.04.12 |
| 통계학 - 확률분포 (0) | 2022.04.12 |
| 통계학 - 확률 (0) | 2022.04.12 |