통계적 추론
표본의 정보로부터 모집단의 특성을 추론
- 모수의 추정(estimation) ex. 점 추정, 구간 추정
- 모수에 대한 가설검정(hypothesis testing)
점추정(point estimation)
모수를 하나의 값으로 추정
모수: 모집단의 평균 𝝁
자료: 평균 𝝁, 표준편차 𝝈인 모집단에서 임의추출한 표본들
추정량: 모수를 추정하는데 이용하는 통계량
확률 변수이므로 모집단에서 관측된 자료에 따라 그 값이 달라질 수 있다.
추정하는 모수와 일치한다고 확신할 수 없다.
추정치: 표본을 이용하여 계산된 추정량의 값
표준오차: 추정치가 모수에 얼마나 가까운지 정확도를 측정하기 위한 도구
모집단의 표준편차 / 루트 표본의 크기
=> 추정치와 그 정확도를 나타내는 표준오차를 함께 제시해야 의미가 있음
구간추정(interval estimation)
모수를 포함할 것으로 기대되는 구간을 이용하여 모수를 추정
신뢰구간(confidence interval): 모수를 추정하는데 이용되는 구간 (L, U)
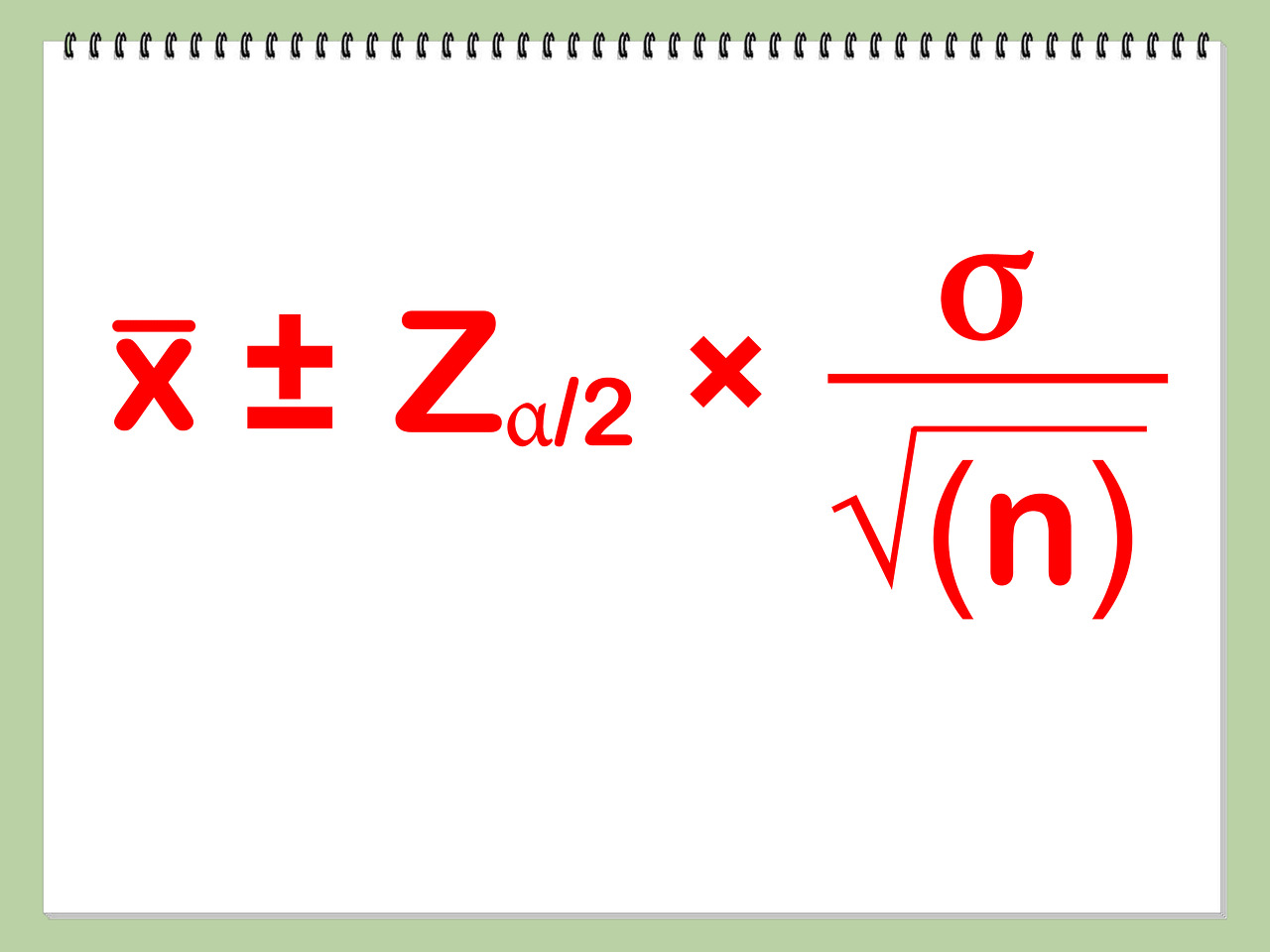
신뢰수준(confidence level): 신뢰구간이 모수를 포함할 확률
같은 신뢰수준에서는 길이가 짧은 신뢰구간이 더 좋음
신뢰구간의 길이가 짧아지는 조건
- 신뢰도 (1-a)가 낮을수록
- 표본의 크기 n이 작을수록
- 표준편차 𝝈가 작을수록
모평균의 추정
일반적으로, 모집단은 그 분포나 표준편차가 알려져 있지 않다.
따라서 모집단의 표준편차를 표본의 표준편차로 대체해서 추정해야 한다.
신뢰구간: 추정량 ± Z𝜶/𝟐 × (추정량의 표준오차)
표본크기의 결정
모평균에 대한 추정에서 오차가 𝒅 이하일 확률이 최소 𝟏 − 𝜶 를 만족하는 최소의 표본 크기
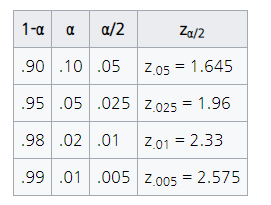
a/2를 이용해 Z값을 추론할 때, z검정의 그래프 모양이 정규분포의 모양임을 기억하자.
자주 쓰이는 값: z0.5=1.645, z.0.25 = 1.96, z.0.1 = 2.33, z.0.05 = 2.575
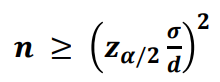
가설검정
모수에 대한 두 가지 가설 중 어느 가설이 타당한지 판단하는 방법
대립가설(alternative hypothesis; 𝑯𝟏) : 새로운 믿음, 입증하고자 하는 가설
귀무가설(null hypothesis; 𝑯𝟎): 기존의 믿음, 대립가설을 입증할 수 없을 때, 대립가설을 무효화시키면서 받아들이는 가설
검정통계량(test statistic): 가설검정에 이용되는 통계량
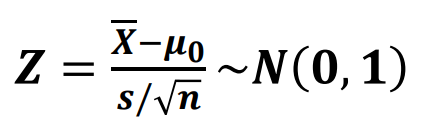
기각역((rejection region): 귀무가설을 기각하는 관측값의 영역
오류의 종류
- 제1종 오류(type I error): 귀무가설이 참일 때, 귀무가설을 기각
- 제2종 오류(type II error): 대립가설이 참일 때, 귀무가설을 기각하지 못함
=> 제1종 오류가 제2종 오류보다 심각함
유의수준(significance level)
제1종 오류를 범할 확률이 우선 작아지도록 기각역을 정함.
즉, 귀무가설하에서 관측값이 기각역에 속할 확률 ex. a = 0.01 or 0.05
Z-검정
vud균이 𝝁, 분산이 𝝈 𝟐인 모집단에서 임의추출한 충분히 큰 크기(𝒏)의 표본
단측검정 => a, 양측검정 => a/2
유의확률((significance probability)
p-value (p-값)
주어진 관측값에 대하여 귀무가설 𝑯𝟎를 기각하게 되는 최소의 유의수준
p-값 < 유의수준 a: 귀무가설 𝑯𝟎 기각
p-값 > 유의수준 a: 귀무가설 𝑯𝟎 기각 불가
'Statistics' 카테고리의 다른 글
| 통계학 - 서술형 대비 개념 정리 (0) | 2022.06.01 |
|---|---|
| 통계학 - 모비율에 대한 통계적 추론 (0) | 2022.05.30 |
| 통계학 - 표집분포 (0) | 2022.05.08 |
| 통계학 (0) | 2022.04.16 |
| 통계학 - 두 변수 자료의 요약 (0) | 2022.04.12 |